Строительные работы в Севастополе
Коэффициент Пуассона (обозначается как ν{\displaystyle \nu } или μ{\displaystyle \mu }) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала[1]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м. Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях. Пусть l{\displaystyle l} и d{\displaystyle d} длина и поперечный размер образца до деформации, а l′{\displaystyle l^{\prime }} и d′{\displaystyle d^{\prime }} — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную (l′−l){\displaystyle (l^{\prime }-l)} , а поперечным сжатием — величину, равную −(d′−d){\displaystyle -(d^{\prime }-d)} . Если (l′−l){\displaystyle (l^{\prime }-l)} обозначить как Δl{\displaystyle \Delta l} , а (d′−d){\displaystyle (d^{\prime }-d)} как Δd{\displaystyle \Delta d} , то относительное продольное удлинение будет равно величине Δll{\displaystyle {\frac {\Delta l}{l}}} , а относительное поперечное сжатие — величине −Δdd{\displaystyle -{\frac {\Delta d}{d}}} . Тогда в принятых обозначениях коэффициент Пуассона μ{\displaystyle \mu } имеет вид: Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся Δll>0{\displaystyle {\frac {\Delta l}{l}}>0} и Δdd<0{\displaystyle {\frac {\Delta d}{d}}<0} , так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении. Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5. Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается. К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20. Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы[2], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0.54), натрий (−0.44), калий (−0.42), кальций (−0.27), медь (−0.13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона. ru-wiki.org Именно поэтому, успех большинства начинаний строительных компаний зависит от грамотного выбора месторасположения строительной площадки. И такой выбор, в свою очередь, невозможен без понимания тех принципов, на которых основывается классификация грунтов.
С точки зрения строительных технологий существуют четыре основных класса, к которым принадлежат:
- скальные грунты, структура которых однородна и основана на жестких связях кристаллического типа;
- дисперсные грунты, состоящие из несвязанных между собой минеральных частиц;
- природные, мерзлые грунты, структура которых образовалась естественным путем, под действием низких температур;
- техногенные грунты, структура которых образовалась искусственным путем, в результате деятельности человека.
Разумеется, в строительном деле пользы от такой классификации немного. Поэтому, каждый тип основания разделяют на несколько классов, групп, типов и разновидностей. Подобная классификация грунтов по группам и разновидностям позволяет без труда сориентироваться в предполагаемых характеристиках будущего основания и дает возможность использовать эти знания в процессе строительства дома.
Например, принадлежность к той или иной группе в классификации грунтов определяется характером структурных связей, влияющих на прочностные характеристики основания. А конкретный тип грунта указывает на вещественный состав почвы. Причем, каждая классификационная разновидность указывает на конкретное соотношение компонентов вещественного состава.
Таким образом, глубокая классификация грунтов по группам и разновидностям дает вполне персонифицированное представление обо всех преимущества и недостатки будущей строительной площадки.
Например, в наиболее распространенном на территории европейской части России классе дисперсных грунтов имеется всего две группы, разделяющие эту классификацию на связанные и несвязанные почвы. Кроме того, в отдельную подгруппу дисперсного класса выделены особые, илистые грунты.
Такая классификация грунтов означает, что среди дисперсных грунтов имеются группы, как с ярко выраженными связями в структуре, так и с отсутствием таковых связей. К первой группе связанных дисперсных грунтов относятся глинистые, илистые и заторфованные виды почвы. Дальнейшая классификация дисперсных грунтов позволяет выделить группу с несвязной структурой – пески и крупнообломочные грунты.
В практическом плане подобная классификация грунтов по группам позволяет получить представление о физических характеристиках почвы «без оглядки» на конкретный вид грунта. У дисперсных связных грунтов практически совпадают такие характеристики, как естественная влажность (колеблется в пределах 20%), насыпная плотность (около 1,5 тонн на кубометр), коэффициент разрыхления (от 1,2 до 1,3), размер частиц (около 0,005 миллиметра) и даже число пластичности.
Аналогичные совпадения характерны и для дисперсных несвязных грунтов. То есть, имея представление о свойствах одного вида грунта, мы получаем сведения о характеристиках всех видов почвы из конкретной группы, что позволяет внедрять в процесс проектирования усредненные схемы, облегчающие прочностные расчеты.
Кроме того, помимо вышеприведенных схем, существует и особая классификация грунтов по трудности разработки. В основе этой классификации лежит уровень «сопротивляемости» грунта механическому воздействию со стороны землеройной техники.
Причем, классификация грунтов по трудности разработки зависит от конкретного вида техники и разделяет все типы грунтов на 7 основных групп, к которым принадлежат дисперсные, связанные и несвязанные грунты (группы 1-5) и скальные грунты (группы 6-7).
Песок, суглинок и глинистые грунты (принадлежат к 1-4 группе) разрабатывают обычными экскаваторами и бульдозерами. А вот остальные участники классификации требуют более решительного подхода, основанного на механическом рыхлении или взрывных работах. В итоге, можно сказать, что классификация грунтов по трудности разработки зависит от таких характеристик, как сцепление, разрыхляемость и плотность грунта.
Модуль деформации определяют испытанием грунта статической нагрузкой, передаваемой на штамп. Испытания проводят в шурфах жестким круглым штампом площадью 5000 см2, а ниже уровня грунтовых вод и на больших глубинах — в скважинах штампом площадью 600 см2. Для определения модуля деформации используют график зависимости осадки от давления, на котором выделяют линейный участок, проводят через него осредняющую прямую и вычисляют модуль деформации Е в соответствии с теорией линейно-деформируемой среды по формуле где v — коэффициент Пуассона (коэффициент поперечной деформации), равный 0,27 для крупнообломочных грунтов, 0,30 для песков и супесей, 0,35 для суглинков и 0,42 для глин; ω — безразмерный коэффициент, равный 0,79; dр — приращение давления на штамп; Δs — приращение осадки штампа, соответствующее Δр. При испытании грунтов необходимо, чтобы толщина слоя однородного грунта под штампом была не менее двух диаметров штампа. Модули деформации изотропных грунтов можно определять в скважинах с помощью прессиометра. В результате испытаний получают график зависимости приращения радиуса скважины от давления на ее стенки. Модуль деформации определяют на участке линейной зависимости деформации от давления между точкой р1, соответствующей обжатию неровностей стенок скважины, и точкой р2E = kr0Δp / Δr
где k — коэффициент; r0 — начальный радиус скважины; Δр — приращение давления; Δr — приращение радиуса, соответствующее Δр. Коэффициент k определяется, как правило, путем сопоставления данных прессиометрии с результатами параллельно проводимых испытаний того же грунта штампом. Для сооружений II и III класса допускается принимать в зависимости от глубины испытания h следующие значения коэффициентов k в формуле: при h < 5 м k = 3; при 5 м ≤ h ≤ 10 м kh ≤ 20 м k = 1,5. Для песчаных и пылевато-глинистых грунтов допускается определять модуль деформации на основе результатов статического и динамического зондирования грунтов. В качестве показателей зондирования принимают: при статическом зондировании — сопротивление грунта погружению конуса зонда qc, а при динамическом зондирований — условное динамическое сопротивление грунта погружению конуса qd. Для суглинков и глин E = 7qc и E = 6qd; для песчаных грунтов E = 3qc, а значения Е по данным динамического зондирования приведены в таблице. Для сооружений I и II класса является обязательным сопоставление данных зондирования с результатами испытаний тех же грунтов штампами. Для сооружений III класса допускается определять Е только по результатам зондирования. В лабораторных условиях применяют компрессионные приборы (одометры), в которых образец грунта сжимается без возможности бокового расширения. Модуль деформации вычисляют на выбранном интервале давлений Δр = p2 − p1 графика испытаний (рис. 1.4) по формуле www.rusconstructor.ru Коэффициент Пуассона (обозначается как ν{\displaystyle \nu } или μ{\displaystyle \mu }) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала[1]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м. Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях. Пусть l{\displaystyle l} и d{\displaystyle d} длина и поперечный размер образца до деформации, а l′{\displaystyle l^{\prime }} и d′{\displaystyle d^{\prime }} — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную (l′−l){\displaystyle (l^{\prime }-l)}, а поперечным сжатием — величину, равную −(d′−d){\displaystyle -(d^{\prime }-d)}. Если (l′−l){\displaystyle (l^{\prime }-l)} обозначить как Δl{\displaystyle \Delta l}, а (d′−d){\displaystyle (d^{\prime }-d)} как Δd{\displaystyle \Delta d}, то ru-wiki.ru Коэффициент Пуассона (обозначается как ν{\displaystyle \nu } или μ{\displaystyle \mu }) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала[1]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м. Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях. Пусть l{\displaystyle l} и d{\displaystyle d} длина и поперечный размер образца до деформации, а l′{\displaystyle l^{\prime }} и d′{\displaystyle d^{\prime }} — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную (l′−l){\displaystyle (l^{\prime }-l)}, а поперечным сжатием — величину, равную −(d′−d){\displaystyle -(d^{\prime }-d)}. Если (l′−l){\displaystyle (l^{\prime }-l)} обозначить как Δl{\displaystyle \Delta l}, а (d′−d){\displaystyle (d^{\prime }-d)} как Δd{\displaystyle \Delta d}, то относительное продольное удлинение будет равно величине Δll{\displaystyle {\frac {\Delta l}{l}}}, а относительное поперечное сжатие — величине −Δdd{\displaystyle -{\frac {\Delta d}{d}}}. Тогда в принятых обозначениях коэффициент Пуассона μ{\displaystyle \mu } имеет вид: Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся Δll>0{\displaystyle {\frac {\Delta l}{l}}>0} и Δdd<0{\displaystyle {\frac {\Delta d}{d}}<0}, так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении. Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5. Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается. К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20. Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы[2], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0,54), натрий (−0,44), калий (−0,42), кальций (−0,27), медь (−0,13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона. Коэффициент Пуассона для грунтов[3]: деформации ν wikiredia.ru Обратимся к рассмотрению деформации твердого тела. В рассматриваемом процессе происходит изменение размеров, объема и часто формы тела. Так, относительное продольное растяжение (сжатие) объекта происходит при его относительном поперечном сужении (расширении). При этом продольная деформация определена формулой: где — длина образца до деформации, — изменение длины при нагрузке. Однако, при растяжении (сжатии) происходит не только изменение длины образца, но и при этом меняются поперечные размеры тела. Деформация в поперечном направлении характеризуется величиной относительного поперечного сужения (расширения): где — диаметр цилиндрической части образца до деформации (поперечный размер образца). Эмпирически получено, что при упругих деформациях выполняется равенство: Коэффициент Пуассона в совокупности с модулем Юнга (E) является характеристикой упругих свойств материала. Если коэффициент объемной деформации () принять равным: где — изменение объема тела, — первоначальный объем тела. То при упругих деформациях выполняется соотношение: Часто в формуле (6) отбрасывают члены малых порядков и используют в виде: Для изотропных материалов коэффициент Пуассона должен находиться в пределах: Существование отрицательных значений коэффициента Пуассона означает, что при растяжении поперечные размеры объекта могли бы увеличиваться. Это возможно при наличии физико-химических изменений в процессе деформации тела. Материалы, у которых коэффициент Пуассона меньше нуля называют ауксетиками. Максимальная величина коэффициента Пуассона является характеристикой более эластичных материалов. Минимальное значение его относится к хрупким веществам. Так стали имеют коэффициент Пуассона от 0,27 до 0,32. Коэффициент Пуассона для резин варьируется в пределах: 0,4 — 0,5. Выражение (4) выполняется и при пластических деформациях, однако в таком случае коэффициент Пуассона зависит от величины деформации: С ростом деформации и возникновении существенных пластических деформаций Опытным путем установлено, что пластическая деформация происходит без изменения объема вещества, так как этот вид деформации возникает за счет сдвигов слоев материала. Коэффициент Пуассона — это физическая величина, не имеющая размерности. ru.solverbook.com Коэффициент Пуассона (часто обозначаемые, как /пи или /ти) – является величиной, в которой отношение относительного поперечного сжатия зависит от относительного продольного растяжения. Коэффициент напрямую зависит не от размера тела, а от природы происхождения материала, породы, из которой происходит данный вид. Коэффициент Пуассона, а также модель Юнга во всех параметрах характеризуют упругие свойства изотропных материалов. Во время приложения на тело растягивающего усилия, образец начинает увеличиваться в продольном направлении, в то время, когда поперечное сечение, наоборот, уменьшается в размерах. Таким образом, коэффициент Пуассона является показателем того, во сколько раз происходит снижение показателя поперечного объема тела, по сравнению с увеличением показателя длины этого самого тела во время растяжения. Само собой, Коэффициент Пуассона для абсолютного хрупкого материала можно выразить показателем – 0. Что касается абсолютно несжимаемого материала, то Коэффициент Пуассона в этом случае равняется 0,5. Скажем так, для большинства стальных объектов показатель примерно 0,3. Резиновые же тела могут достигать коэффициента 0,5. Для этой величины можно указывать единицы измерения в мм \мм, м\м. Само собой, существуют и такие материалы, у которых Коэффициент Пуассона имеет отрицательную величину. Это, как правило, полимеры - их так же называют ауксетиками. Они встречаются очень редко. Это означает, то, что во время того, как к таким телам прикладывается растягивающее усилие, их поперечное сечения начинает увеличиваться. Если рассматривать бумагу, состоящую из однослойных нанотрубок, то она имеет положительный показатель коэффициент Пуассона. Однако в том случае, если доли многослойных нанотрубок увеличить, то сразу становится заметна быстрая замена на отрицательное значение до -0,20. Многие анизотропные кристаллы имеют как раз-таки отрицательный коэффициент Пуассона, а зависит это от угла ориентации структуры кристалла относительно его оси растяжения. К таким материалам с отрицательными показателями относится: • -0,54 – показатель лития • -0,44 – показатель натрия • - 0,42 – показатель калия • - 0,27 – показатель кальция • - 0,13 – показатель меди. Далее по списку остальные 67% кристаллов, имеющихся в таблице Менделеева, с отрицательным v коэффициентом Пуассона. Существует специальная таблица для того, чтобы определить Коэффициент Пуассона для грунтов. От 0.20 до 0.30 От 0.30 до 0.38 От 0.38 до 0.45 Чем больше значение плотности грунта, тем меньшие значения применяются. specural.com Коэффициент Пуассона (обозначается как или ) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала[1]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м. Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях. Пусть и длина и поперечный размер образца до деформации, а и — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную , а поперечным сжатием — величину, равную . Если обозначить как , а как , то относительное продольное удлинение будет равно величине , а относительное поперечное сжатие — величине . Тогда в принятых обозначениях коэффициент Пуассона имеет вид: Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся и , так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении. Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5. Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается. К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20. Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы[2], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0.54), натрий (−0.44), калий (−0.42), кальций (−0.27), медь (−0.13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона. Коэффициент Пуассона для грунтов[3]: деформации ν www.wikiznanie.ruКоэффициент Пуассона. Коэффициент пуассона для грунтов
Коэффициент Пуассона — WiKi
Эта статья — о параметре, характеризующем упругие свойства материала. О понятии в термодинамике см. Показатель адиабаты. Классификация видов грунтов по своим группам
От надежности функционирования системы «основание-фундамент-сооружение» зависит и срок эксплуатации здания, и уровень «качества жизни» его жильцов. Причем, надежность указанной системы базируется именно на характеристиках грунта, ведь любая конструкция должна опираться на надежное основание. ГЕНЕТИЧЕСКИЕ ТИПЫ ГРУНТОВ ЧЕТВЕРТИЧНОГО ВОЗРАСТА
Типы грунтов Обозначение Аллювиальные (речные отложения) a Озерные l Озерно-аллювиальные lа Делювиальные (отложения дождевых и талых вод на склонах и у подножия возвышенностей)
d Аллювиально-делювиальные ad Эоловые (осаждения из воздуха): эоловые пески, лессовые грунты L Гляциальные (ледниковые отложения) g Флювиогляциальные (отложении ледниковых потоков) f Озерно-ледниковые lg Элювиальные (продукты выветривания горных пород, оставшиеся на месте образования) е Элювиально-делювиальное ed Пролювиальные (отложения бурных дождевых потоков в горных областях) p Аллювиально-пролювиальные ap Морские m РАСЧЕТНЫЕ ФОРМУЛЫ ОСНОВНЫХ ФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ГРУНТОВ
Характеристики
Формула
Плотность сухого грунта, г/см3 (т/м3)
ρd = ρ/(1 + w)
Пористость %
n = (1 − ρd /ρs)·100
Коэффициент пористости
e = n/(100 − n) или e = (ρs − ρd)/ ρd
Полная влагоемкость
ω0 = eρw /ρs
Степень влажности
Число пластичности
Ip = ωL − ωp
Показатель текучести
IL = (ω − ωp)/(ωL − ωp)
ПЛОТНОСТЬ ЧАСТИЦ ρs ПЕСЧАНЫХ И ПЫЛЕВАТО-ГЛИНИСТЫХ ГРУНТОВ
Грунт
ρs, г/см3
диапазон
средняя
Песок
2,65–2,67
2,66
Супесь
2,68–2,72
2,70
Суглинок
2,69–2,73
2,71
Глина
2,71–2,76
2,74
КЛАССИФИКАЦИЯ СКАЛЬНЫХ ГРУНТОВ
Грунт
Показатель
По пределу прочности на одноосное сжатие в водонасыщенном состоянии, МПа
Очень прочный
Rc > 120
Прочный
120 ≥ Rc > 50
Средней прочности
50 ≥ Rc > 15
Малопрочный
15 ≥ Rc > 5
Пониженной прочности
5 ≥ Rc > 3
Низкой прочности
3 ≥ Rc ≥ 1
Весьма низкой прочности
Rc < 1
По коэффициенту размягчаемости в воде
Неразмягчаемый
Ksaf ≥ 0,75
Размягчаемый
Ksaf < 0,75
По степени растворимости в воде (осадочные сцементированные), г/л
Нерастворимый
Растворимость менее 0,01
Труднорастворимый
Растворимость 0,01—1
Среднерастворимый
− || − 1—10
Легкорастворимый
− || − более 10
КЛАССИФИКАЦИЯ КРУПНООБЛОМОЧНЫХ И ПЕСЧАНЫХ ГРУНТОВ ПО ГРАНУЛОМЕТРИЧЕСКОМУ СОСТАВУ
Грунт
Размер частиц, мм
Масса частиц, % от массывоздушно-сухого грунта
Крупнообломочный: валунный (глыбовый) галечниковый (щебенистый) гравийный (дресвяный)
>200>10>2
>50
Песок: гравелистый крупный средней крупности мелкий пылеватый
>2>0,5>0,25>0,1>0,1
>25>50>50≥75<75
ПОДРАЗДЕЛЕНИЕ КРУПНООБЛОМОЧНЫХ И ПЕСЧАНЫХ ГРУНТОВ ПО СТЕПЕНИ ВЛАЖНОСТИ Sr
Грунт
Степень влажности
Маловлажный
0 < Sr ≤ 0,5
Влажный
0,5 < Sr ≤ 0,8
Насыщенный водой
0,8 < Sr ≤ 1
ПОДРАЗДЕЛЕНИЕ ПЕСЧАНЫХ ГРУНТОВ ПО ПЛОТНОСТИ СЛОЖЕНИЯ
Песок
Подразделение по плотности сложения
плотный
средней плотности
рыхлый
По коэффициенту пористости
Гравелистый, крупный и средней крупности
e < 0,55
0,55 ≤ e ≤ 0,7
e > 0,7
Мелкий
e < 0,6
0,6 ≤ e ≤ 0,75
e > 0,75
Пылеватый
e < 0,6
0,6 ≤ e ≤ 0,8
e > 0,8
По удельному сопротивлению грунта, МПа, под наконечником (конусом) зонда при статическом зондировании
Крупный и средней крупности независимо от влажности
qc > 15
15 ≥ qc ≥ 5
qc < 5
Мелкий независимо от влажности
qc > 12
12 ≥ qc ≥ 4
qc < 4
Пылеватый: маловлажный и влажный водонасыщенный
qc > 10qc > 7
10 ≥ qc ≥ 37 ≥ qc ≥ 2
qc < 3qc < 2
По условному динамическому сопротивлению грунта МПа, погружению зонда при динамическом зондировании
Крупный и средней крупности независимо от влажности
qd > 12,5
12,5 ≥ qd ≥ 3,5
qd < 3,5
Мелкий: маловлажный и влажный водонасыщенный
qd > 11qd > 8,5
11 ≥ qd ≥ 38,5 ≥ qd ≥ 2
qd < 3qd < 2
Пылеватый маловлажный и влажный
qd > 8,8
8,5 ≥ qd ≥ 2
qd < 2
ПОДРАЗДЕЛЕНИЕ ПЫЛЕВАТО-ГЛИНИСТЫХ ГРУНТОВ ПО ЧИСЛУ ПЛАСТИЧНОСТИ
Грунт
Число пластичности, %
Супесь
1 < Ip ≤ 7
Суглинок
7 < Ip ≤ 17
Глина
Ip > 17
ПОДРАЗДЕЛЕНИЕ ПЫЛЕВАТО-ГЛИНИСТЫХ ГРУНТОВ ПО ПОКАЗАТЕЛЮ ТЕКУЧЕСТИ
Грунт
Показатель текучести
Супесь:
IL < 0
пластичная
0 ≤ IL ≤ 1
текучая
IL > 1
Суглинок и глина:
твердые
IL < 0
полутвердые
0 ≤ IL ≤ 0,25
тугопластичные
0,25 ≤ IL ≤ 0,5
мягкопластичные
0,5 ≤ IL ≤ 0,75
текучепластичные
0,75 ≤ IL ≤ 1
текучие
IL > 1
ПОДРАЗДЕЛЕНИЕ ИЛОВ ПО КОЭФФИЦИЕНТУ ПОРИСТОСТИ
Ил
Коэффициент пористости
Супесчаный
е ≥ 0,9
Суглинистый
е ≥ 1
Глинистый
е ≥ 1,5
ПОДРАЗДЕЛЕНИЕ САПРОПЕЛЕЙ ПО ОТНОСИТЕЛЬНОМУ СОДЕРЖАНИЮ ОРГАНИЧЕСКОГО ВЕЩЕСТВА
Сапропель
Относительное содержание вещества
Минеральный
0,1 < Iот ≤ 0,3
Среднеминеральный
0,3 < Iот ≤ 0,5
Слабоминеральный
Iот > 0,5
НОРМАТИВНЫЕ ЗНАЧЕНИЯ МОДУЛЕЙ ДЕФОРМАЦИИ Е ПЫЛЕВАТО-ГЛИНИСТЫХ ГРУНТОВ
Возраст и происхождение грунтов
Грунт
Показатель текучести
Значения Е, МПа, при коэффициенте пористости е
0,35
0,45
0,55
0,65
0,75
0,85
0,95
1,05
1,2
1,4
1,6
Четвертичные отложения: иллювиальные, делювиальные, озерно-аллювиальные
Супесь
0 ≤ IL ≤ 0,75
–
32
24
16
10
7
–
–
–
–
–
Суглинок
0 ≤ IL ≤ 0,25
–
34
27
22
17
14
11
–
–
–
–
0,25 < IL ≤ 0,5
–
32
25
19
14
11
8
–
–
–
–
0,5 < IL ≤ 0,75
–
–
–
17
12
8
6
5
–
–
–
Глина
0 ≤ IL ≤ 0,25
–
–
28
24
21
18
15
12
–
–
–
0,25 < IL ≤ 0,5
–
–
–
21
18
15
12
9
–
–
–
0,5 < IL ≤ 0,75
–
–
–
–
15
12
9
7
–
–
–
флювиогляциальные
Супесь
0 ≤ IL ≤ 0,75
–
33
24
17
11
7
–
–
–
–
–
Суглинок
0 ≤ IL ≤ 0,25
–
40
33
27
21
–
–
–
–
–
–
0,25<IL≤0,5
–
35
28
22
17
14
–
–
–
–
–
0,5 < IL ≤ 0,75
–
–
–
17
13
10
7
–
–
–
–
моренные
Супесь и суглинок
IL ≤ 0,5
75
55
45
–
–
–
–
–
–
–
–
Юрские отложения оксфордского яруса
Глина
− 0,25 ≤ IL ≤ 0
–
–
–
–
–
–
27
25
22
–
–
0 < IL ≤ 0,25
–
–
–
–
–
–
24
22
19
15
–
0,25 < IL ≤ 0,5
–
–
–
–
–
–
–
–
16
12
10
Определение модуля деформации в полевых условиях
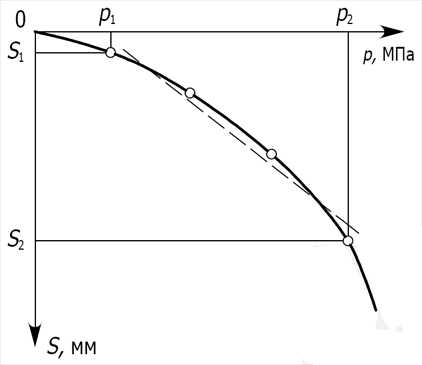
Зависимость осадки штампа s от давления р
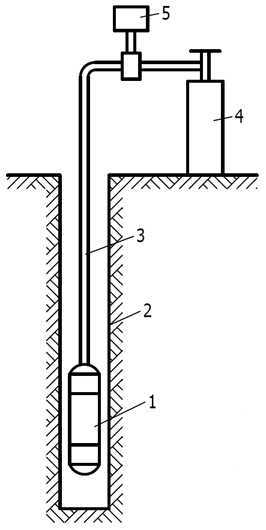
Схема испытания грунта прессиометром
1 — резиновая камера; 2 — скважина; 3 — шланг; 4 — баллон сжатого воздуха: 5 — измерительное устройство 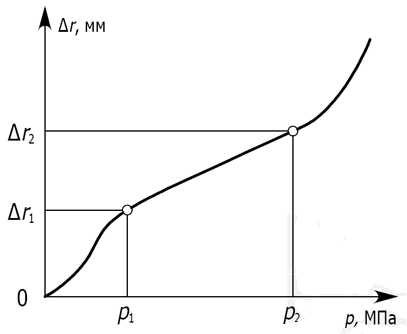
Зависимость деформаций стенок скважины Δr от давления р
ЗНАЧЕНИЯ МОДУЛЕЙ ДЕФОРМАЦИИ Е ПЕСЧАНЫХ ГРУНТОВ ПО ДАННЫМ ДИНАМИЧЕСКОГО ЗОНДИРОВАНИЯ
Песок
Значения Е, МПа, при qd, МПа
2
3,5
7
11
14
17,5
Крупный и средней крупности
20–16
26–21
39–34
49–44
53–50
60–55
Мелкий
13
19
29
35
40
45
Пылеватый (кроме водонасыщенных)
8
13
22
28
32
35
СРЕДНИЕ ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ПУАССОНА vβ
Грунт
ν
β = 1 − 2ν2 / (1 − ν)
Песок и супесь
0,30
0,74
Суглинок
0,35
0,62
Глина
0,42
0,40
КОЭФФИЦИЕНТЫ m ДЛЯ АЛЛЮВИАЛЬНЫХ, ДЕЛЮВИАЛЬНЫХ, ОЗЕРНЫХ И ОЗЕРНО-АЛЛЮВИАЛЬНЫХ ЧЕТВЕРТИЧНЫХ ГРУНТОВ ПРИ ПОКАЗАТЕЛЕ ТЕКУЧЕСТИ IL ≤ 0,75
Грунт
Значения m при коэффициенте пористости e
0,45
0,55
0,65
0,75
0,85
0,95
1,05
Супесь
4,0
4,0
3,5
3,0
2,0
–
–
Суглинок
5,0
5,0
4,5
4,0
3,0
2,5
2,0
Глина
–
–
6,0
6,0
5,5
5,0
4,5
НОРМАТИВНЫЕ ЗНАЧЕНИЯ УДЕЛЬНЫХ СЦЕПЛЕНИИ c, кПа, И УГЛОВ ВНУТРЕННЕГО ТРЕНИЯ φ, град, ПЕСЧАНЫХ ГРУНТОВ
Песок
Характеристика
Значения с и φ при коэффициенте пористости e
0,45
0,55
0,65
0,75
Гравелистый и крупный
сφ
243
140
038
––
Средней крупности
сφ
340
238
135
––
Мелкий
сφ
638
436
232
028
Пылеватый
сφ
836
634
430
226
НОРМАТИВНЫЕ ЗНАЧЕНИЯ УДЕЛЬНЫХ СЦЕПЛЕНИЯ c, кПа, И УГЛОВ ВНУТРЕННЕГО ТРЕНИЯ φ, град, ПЫЛЕВАТО-ГЛИНИСТЫХ ГРУНТОВ ЧЕТВЕРТИЧНЫХ ОТЛОЖЕНИЙ
Грунт
Показатель текучести
Характеристика
Значения с и φ при коэффициенте пористости е
0,45
0,55
0,65
0,75
0,85
0,95
1,05
Супесь
0<IL≤0,25
сφ
2130
1729
1527
1324
––
––
––
0,25<IL≤0,75
сφ
1928
1526
1324
1121
918
––
––
Суглинок
0<IL≤0,25
сφ
4726
3725
3124
2523
2222
1920
––
0,25<IL≤0,5
сφ
3924
3423
2822
2321
1819
1517
––
0,5<IL≤0,75
сφ
––
––
2519
2018
1616
1414
1212
Глина
0<IL≤0,25
сφ
––
8121
6820
5419
4718
4116
3614
0,25<IL≤0,5
сφ
––
––
5718
5017
4316
3714
3211
0,5<IL≤0,75
сφ
––
––
4515
4114
3612
3310
297
ЗНАЧЕНИЯ УГЛОВ ВНУТРЕННЕГО ТРЕНИЯ φ ПЕСЧАНЫХ ГРУНТОВ ПО ДАННЫМ ДИНАМИЧЕСКОГО ЗОНДИРОВАНИЯ
Песок
Значения φ, град, МПа при qd, МПа
2
3,5
7
11
14
17,5
Крупный и средней крупности
30
33
33
38
40
41
Мелкий
28
30
33
35
37
38
Пылеватый
28
28
30
32
34
35
ОРИЕНТИРОВОЧНЫЕ ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ФИЛЬТРАЦИИ ГРУНТОВ
Грунт
k, м/сут
Галечниковый (чистый)
>200
Гравийный (чистый)
100–200
Крупнообломочный с песчаным заполнителем
100–150
Песок: гравелистый крупный средней крупности мелкий пылеватый
50–10025–7510–252–100,1–2
Супесь
0,1–0,7
Суглинок
0,005–0,4
Глина
<0,005
Торф: слаборазложившийся среднеразложившийся сильноразложившийся
1–40,15–10,01–0,15
ЗНАЧЕНИЯ СТАТИСТИЧЕСКОГО КРИТЕРИЯ
Числоопределений
v
Числоопределений
v
Числоопределений
v
6
2,07
13
2,56
20
2,78
7
2,18
14
2,60
25
2,88
8
2,27
15
2,64
30
2,96
9
2,35
16
2,67
35
3,02
10
2,41
17
2,70
40
3,07
11
2,47
18
2,73
45
3,12
12
2,52
19
2,75
50
3,16
ТАБЛИЦА 1.22. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА tα ПРИ ОДНОСТОРОННЕЙ ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТИ α
Число
определенийn−1 или n−2
tα при α
Число
определенийn−1 или n−2
tα при α
0,85
0,95
0,85
0,95
2
1,34
2,92
13
1,08
1,77
3
1,26
2,35
14
1,08
1,76
4
1,19
2,13
15
1,07
1,75
5
1,16
2,01
16
1,07
1,76
6
1,13
1,94
17
1,07
1,74
7
1,12
1,90
18
1,07
1,73
8
1,11
1,86
19
1,07
1,73
9
1,10
1,83
20
1,06
1,72
10
1,10
1,81
30
1,05
1,70
11
1,09
1,80
40
1,06
1,68
12
1,08
1,78
60
1,05
1,67
Коэффициент Пуассона Википедия
Эта статья — о параметре, характеризующем упругие свойства материала. О понятии в термодинамике см. Показатель адиабаты. Детальное определение[ | код]
Однородный стержень до и после приложения к нему растягивающих сил. Коэффициент Пуассона Википедия
Эта статья — о параметре, характеризующем упругие свойства материала. О понятии в термодинамике см. Показатель адиабаты. Детальное определение
Однородный стержень до и после приложения к нему растягивающих сил. Ауксетики
Значения коэффициента Пуассона
Грунты
Грунты Коэффициент поперечной Крупнообломочные грунты 0,27 Пески и супеси 0,30 — 0,35 Суглинки 0,35 — 0,37 Глины при показателе текучести IL IL < 0 0 < IL <= 0,25 0,25 < IL <= 1 0,20 — 0,30 0,30 — 0,38 0,38 — 0,45 Примечание. Меньшие значения ν применяют при большей плотности грунта. Изотропные материалы
Материал Коэффициент Пуассона μ Бетон 0,2 по СНиП, в расчётах возможно снижение до 0,15—0,17 Алюминий 0,34 Вольфрам 0,29 Германий 0,31 Дюралюминий 0,34 Иридий 0,26 Кварцевое стекло 0,17 Константан 0,33 Латунь 0,35 Манганин 0,33 Медь 0,35 Органическое стекло 0,35 Полистирол 0,35 Свинец 0,44 Олово 0,44 Серебро 0,37 Серый чугун 0,22 Сталь 0,25 Стекло 0,25 Фарфор 0,23 Примечания
См. также
Коэффициент Пуассона, формула и примеры
Определение и формула коэффициента Пуассона
Коэффициент Пуассона при объемной деформации
Коэффициент Пуассона и пластическая деформация
Единицы измерения
Примеры решения задач
Коэффициент Пуассона для грунтов - Разное
Что означает этот показатель
Материалы с отрицательным значением Коэффициента Пуассона
Показатели некоторых антиизотопных кристаллов
Грунты Коэффициент поперечной деформации ν Крупнообломочные грунты Равен 0,27 Супесь и песок 0,30 — 0,35 Суглинка 0,35 — 0,37 Глины с учетом текучести IL IL < 0 0 < IL <= 0,25 0,25 < IL <= 1 Коэффициент Пуассона — Википедия
Эта статья — о параметре, характеризующем упругие свойства материала. О понятии в термодинамике см. Показатель адиабаты. Детальное определение[править]
Однородный стержень до и после приложения к нему растягивающих сил. Значения коэффициента Пуассона[править]
Грунты[править]
Грунты Коэффициент поперечной Крупнообломочные грунты 0,27 Пески и супеси 0,30 — 0,35 Суглинки 0,35 — 0,37 Глины при показателе текучести IL IL < 0 0 < IL <= 0,25 0,25 < IL <= 1 0,20 — 0,30 0,30 — 0,38 0,38 — 0,45 Примечание. Меньшие значения ν применяют при большей плотности грунта. Изотропные материалы[править]
Материал Коэффициент Пуассона μ Бетон 0,2 по СНиП, в расчётах возможно снижение до 0,15—0,17 Алюминий 0,34 Вольфрам 0,29 Германий 0,31 Дюралюминий 0,34 Иридий 0,26 Кварцевое стекло 0,17 Константан 0,33 Латунь 0,35 Манганин 0,33 Медь 0,35 Органическое стекло 0,35 Полистирол 0,35 Свинец 0,44 Олово 0,44 Серебро 0,37 Серый чугун 0,22 Сталь 0,28 Стекло 0,25 Фарфор 0,23