Строительные работы в Севастополе
При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит название чистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу. Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называется нейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки. Нейтральная линия — это линия, в которой нормальные напряжения равны нулю. Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе. Допущения для вывода формул нормального напряжения: 1) Выполняется гипотеза плоских сечений. 2) Продольные волокна друг на друга не давят (гипотеза о ненадавливании) и, следовательно, каждое из волокон находится в состоянии одноосного растяжения или сжатия. 3) Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми. 4) Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости. 5) Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков. 6) Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания. Рассмотрим балку произвольного сечения, но имеющую ось симметрии. Формула (1) выражает статическую сторону задачи об изгибе прямого бруса, но по ней по известному изгибающему моменту нельзя определить нормальные напряжения, пока не установлен закон их распределения. Выделим на среднем участке балки и рассмотрим участок длиной dz, подвергающийся изгибу. Изобразим его в укрупненном масштабе. К выводу формул при изгибе: а) участок балки до деформации; б) участок балки после деформации Сечения, ограничивающие участок dz, параллельны друг другу до деформации, а после приложения нагрузки повернутся вокруг своих нейтральных линий на угол Теперь перейдем к напряжениям, т.е. будем рассматривать физическую сторону задачи. в соответствии с допущением о ненадавливании волокон используем закон Гука при осевом растяжении-сжатии: Тогда Подставим полученное выражение кривизны (4) в выражение (3) и получим формулу для вычисления нормальных напряжений в любой точке поперечного сечения: Т.о. максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии. Отношение Тогда максимальные напряжения: Условие прочности при изгибе: При поперечном изгибе действуют не только нормальные, но и касательные напряжения,т.к. имеется поперечная сила. Касательные напряжения усложняют картину деформирования, они приводят к искривлению поперечных сечений балки, в результате чего нарушается гипотеза плоских сечений. Однако исследования показывают, что искажения, которые привносят касательные напряжения, незначительно влияют на нормальные напряжения,подсчитанные по формуле (5). Таким образом ,при определении нормальных напряжений в случае поперечного изгиба теория чистого изгиба вполне применима. Нейтральная линия. Вопрос о положении нейтральной линии. При изгибе отсутствует продольная сила, поэтому можно записать Условие Установив положение нейтральной линии, несложно построить эпюру нормальных напряжений по высоте сечения. Ее линейный характер определяется уравнением первой степени. Характер эпюры σ для симметричных сечений относительно нейтральной линии, М<0 www.prosopromat.ru Деформация изгиба характеризуется потерей прямолинейности или первоначальной формы линией балки (ее осью) при приложении внешней нагрузки. При этом, в отличие от деформации сдвига, линия балки изменяет свою форму плавно.
Легко убедиться, что на сопротивляемость изгибу влияет не только площадь поперечного сечения балки (бруса, стержня и т. д.), но и геометрическая форма этого сечения. Поскольку изгиб тела (балки, бруса и т. п.) осуществляется относительно какой-либо оси, на сопротивляемость изгибу влияет величина осевого момента инерции сечения тела относительно этой оси.
Для сравнения - при деформации кручения сечение тела подвергается закручиванию относительно полюса (точки), поэтому на сопротивление кручению оказывает влияние полярный момент инерции этого сечения. На изгиб могут работать многие элементы конструкций – оси, валы, балки, зубья зубчатых колес, рычаги, тяги и т. д. В сопротивлении материалов рассматривают несколько типов изгибов:
- в зависимости от характера внешней нагрузки, приложенной к брусу, различают чистый изгиб и поперечный изгиб;
- в зависимости от расположения плоскости действия изгибающей нагрузки относительно оси бруса - прямой изгиб и косой изгиб. *** Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент (рис. 2).
Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил. Тогда в каждом сечении бруса будут действовать только изгибающие моменты. Если же изгиб имеет место в результате приложения к брусу поперечной силы (рис. 3), то такой изгиб называется поперечным. В этом случае в каждом сечении бруса действует и поперечная сила, и изгибающий момент (кроме сечения, к которому приложена внешняя нагрузка). Если брус имеет хоть одну ось симметрии, и плоскость действия нагрузок совпадает с ней, то имеет место прямой изгиб, если же это условие не выполняется, то имеет место косой изгиб. При изучении деформации изгиба будем мысленно представлять себе, что балка (брус) состоит из бесчисленного количества продольных, параллельных оси волокон.
Чтобы наглядно представить деформацию прямого изгиба, проведем опыт с резиновым брусом, на котором нанесена сетка продольных и поперечных линий.
Подвергнув такой брус прямому изгибу, можно заметить, что (рис. 1): - поперечные линии останутся при деформации прямыми, но повернутся под углом друг другу;
- сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне;
- продольные прямые линии искривятся. Из этого опыта можно сделать вывод, что: - при чистом изгибе справедлива гипотеза плоских сечений;
- волокна, лежащие на выпуклой стороне растягиваются, на вогнутой стороне – сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины. Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью. Очевидно, что на нейтральной оси нормальные напряжения равны нулю. *** Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. При решении задач сопротивления материалов, и определении внутренних силовых факторов в брусьях, мы учитывали реакции связей наравне с внешними нагрузками, действующими на брусья.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей). Рассмотрим два случая: 1. К балке приложены две равные и противоположные по знаку пары сил.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1-1 (рис. 2), видим, что во всех поперечных сечениях возникает только изгибающий момент Ми, равный внешнему моменту. Таким образом, это случай чистого изгиба. Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки. Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента. 2. К балке приложены активные и реактивные силы (нагрузки и реакции связей), перпендикулярные оси (рис. 3). Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий момент Ми и поперечная сила Q.
Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе. Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки. Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы. Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным. У балки, находящейся в равновесии вод действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих на балку справа или слева от сечения. У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т. е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно сумма внешних сил, действующих на балку левее сечения, численно равна алгебраической сумме сил, действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения. Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно:
Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (рис 4,a). Если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4,b).
Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемлённым, а связи отброшенными и замененными реакциями. Еще раз отметим, что для определения реакций связей пользуются правилами знаков статики, а для определения знаков изгибающего момента и поперечной силы – правилами знаков сопротивления материалов.
Правило знаков для изгибающих моментов иногда называют "правилом дождя", имея в виду, что в случае выпуклости вниз образуется воронка, в которой задерживается дождевая вода (знак положительный), и наоборот – если под действием нагрузок балка выгибается дугой вверх, вода на ней не задерживается (знак изгибающих моментов отрицательный). *** Материалы раздела "Изгиб": Деформация кручения № вопроса 1 2 3 4 5 6 7 8 9 10 Правильный вариант ответа 3 1 3 2 3 2 2 1 2 3 k-a-t.ru Изгибом называется деформация, при которой ось стержня и все его волокна, т. е. продольные линии, параллельные оси стержня, искривляются под действием внешних сил. Наиболее простой случай изгиба получается тогда, когда внешние силы будут лежать в плоскости, проходящей через центральную ось стержня, и не дадут проекций на эту ось. Такой случай изгиба называют поперечным изгибом. Различают плоский изгиб и косой. Плоский изгиб – такой случай, когда изогнутая ось стержня расположена в той же плоскости, в которой действуют внешние силы. Косой (сложный) изгиб – такой случай изгиба, когда изогнутая ось стержня не лежит в плоскости действия внешних сил. Работающий на изгиб стержень обычно называют балкой. При плоском поперечном изгибе балок в сечении с системой координат у0х могут возникать два внутренних усилия – поперечная сила Qу и изгибающий момент Мх; в дальнейшем для них вводятся обозначения Q и M. Если в сечении или на участке балки поперечная сила отсутствует (Q=0), а изгибающий момент не равен нулю или М – const, то такой изгиб принято называть чистым. Поперечная сила в каком-либо сечении балки численно равна алгебраической сумме проекций на ось у всех сил (включая опорные реакции), расположенных по одну сторону (любую) от проведенного сечения. Изгибающий момент в сечении балки численно равен алгебраической сумме моментов всех сил (включая и опорные реакции), расположенных по одну сторону (любую) от проведенного сечения относительно центра тяжести этого сечения, точнее, относительно оси, проходящей перпендикулярно плоскости чертежа через центр тяжести проведенного сечения. Сила Q представляет равнодействующую распределенных по сечению внутренних касательных напряжений, а момент М– сумму моментов вокруг центральной оси сечения Х внутренних нормальных напряжений. Между внутренними усилиями существует дифференциальная зависимость которая используется при построении и проверке эпюр Q и M. Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называется нейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки. Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений. Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе. Поперечное сечение балки при изгибе искажается. За счет поперечной деформации размеры поперечного сечения в сжатой зоне балки увеличиваются, а в растянутой сжимаются. Допущения для вывода формул. Нормальные напряжения 1) Выполняется гипотеза плоских сечений. 2) Продольные волокна друг на друга не давят и, следовательно, под действием нормальных напряжений линейные растяжения или сжатия работают. 3) Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми. 4) Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости. 5) Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков. 6) Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания. При чистом изгибе балки на площадках в ее сечении действуют только нормальные напряжения, определяемые по формуле : где у – координата произвольной точки сечения, отчитываемая от нейтральной линии — главной центральной оси х. Нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Характер эпюр нормальных напряжений для симметричных сечений относительно нейтральной линии Характер эпюр нормальных напряжений для сечений, не обладающих симметрией относительно нейтральной линии Опасными являются точки, наиболее удаленные от нейтральной линии. Выберем некоторое сечение Для любой точки сечения,назовем ее точкой К, условие прочности балки по нормальным напряжениям имеет вид: это осевой момент сопротивления сечения относительно нейтральной оси. Его размерность см3, м3. Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений. Условие прочности по нормальным напряжениям: Если материал неодинаково сопротивляется растяжению и сжатию, то необходимо использовать два условия прочности: для зоны растяжения с допускаемым напряжением на растяжение; для зоны сжатия с допускаемым напряжением на сжатие . При поперечном изгибе балки на площадках в ее сечении действуют как нормальные, так и касательные напряжения. В случае изгиба, когда присутствует поперечная сила, сечения не будут плоскими. Они будут искривляться. Но опытные данные показывают, что искривления небольшие, поэтому применяют формулу чистого изгиба для определения нормальных напряжений. Для определения касательных напряжений используется выражение, называемое в отечественной литературе формулой Д.И.Журавского: Условие прочности по касательным напряжениям: www.prosopromat.ru Проектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано: Покажем балку с построенными эпюрами Q и М Согласно эпюре изгибающих моментов опасным является сечение С, в котором МС=Мmax=48,3кНм. Условие прочности по нормальным напряжениям для данной балки имеет вид σmax=MC/WX≤σadm. Требуется подобрать сечение из двух швеллеров. Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера Ix=1670см4, тогда осевой момент сопротивления всего сечения: Перенапряжение (недонапряжение) в опасных точках посчитаем по формуле: Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям. Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН. Условие прочности по касательным напряжениям имеет вид: Для швеллера №20 а: статический момент площади Sx1=95,9 см3, момент инерции сечения Ix1=1670 см4, толщина стенки d1=5,2 мм, средняя толщина полки t1=9,7 мм, высота швеллера h2=20 см, ширина полки b1=8 см. Для поперечного сечения из двух швеллеров: Sx= 2Sx1=2·95,9=191,8 см3, Ix=2Ix1=2·1670=3340 см4, b=2d1=2·0,52=1,04 см. Определяем значение максимального касательного напряжения: τmax=48,9·103·191,8·10−6/3340·10−8·1,04·10−2=27МПа. Как видно, τmax <τadm (27МПа<75МПа). Следовательно, условие прочности выполняется. Проверяем прочность балки по энергетическому критерию. Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют MC=Mmax=48,3 кНм и QC=Qmax=48,9 кН. Проведем анализ напряженного состояния в точках сечения С Схема сечения балки и эпюры напряжений для анализа напряженного состояния Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения) Уровень 1-1: y1-1=h2/2=20/2=10см. Нормальные и касательные напряжения: Главные напряжения: Экстремальные касательные напряжения: Уровень 2−2: y2-2=h2/2−t1=20/2−0,97=9,03см. Нормальные и касательные напряжения: Главные напряжения: Экстремальные касательные напряжения: Уровень 3−3: y3-3=h2/2−t1=20/2−0,97=9,03см. Нормальные и касательные напряжения: Главные напряжения: Экстремальные касательные напряжения: Уровень 4−4: y4-4=0. Нормальные и касательные напряжения: Главные напряжения: Экстремальные касательные напряжения: Уровень 5−5: Нормальные и касательные напряжения: Главные напряжения: Экстремальные касательные напряжения: Уровень 6−6: Нормальные и касательные напряжения: Главные напряжения: Экстремальные касательные напряжения: Уровень 7−7: Нормальные и касательные напряжения: Главные напряжения: Экстремальные касательные напряжения: В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ1, σ3, τmax и τmin представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых: Используя энергетический критерий прочности, получим Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется (135,3 МПа<150 МПа). www.prosopromat.ru Деформация изгибазаключается в искривлении оси прямого стержня или в изменении начальной кривизны прямого стержня (рис. 6.1). Ознакомимся с основными понятиями, которые используются при рассмотрении деформации изгиба. Стержни, работающие на изгиб, называют балками. Чистымназывается изгиб, при котором изгибающий момент является единственным внутренним силовым фактором, возникающем в поперечном сечении балки. Чаще, в поперечном сечении стержня наряду с изгибающим моментом возникает также и поперечная сила. Такой изгиб называют поперечным. Плоским (прямым)называют изгиб, когда плоскость действия изгибающего момента в поперечном сечении проходит через одну из главных центральных осей поперечного сечения. При косом изгибеплоскость действия изгибающего момента пересекает поперечное сечение балки по линии, не совпадающей ни с одной из главных центральных осей поперечного сечения. Изучение деформации изгиба начнем со случая чистого плоского изгиба. Как уже было сказано, при чистом плоском изгибе в поперечном сечении из шести внутренних силовых факторов не равен нулю только изгибающий момент (рис. 6.1, в): ; (6.1) Опыты, поставленные на эластичных моделях, показывают, что если на поверхность модели нанести сетку линий (рис. 6.1, а), то при чистом изгибе она деформируется следующим образом (рис. 6.1, б): а) продольные линии искривляются по длине окружности; б) контуры поперечных сечений остаются плоскими; в) линии контуров сечений всюду пересекаются с продольными волокнами под прямым углом. На основании этого можно предположить, что при чистом изгибе поперечные сечения балки остаются плоскими и поворачиваются так, что остаются нормальными к изогнутой оси балки (гипотеза плоских сечений при изгибе). Рис. 6.1 Замеряя длину продольных линий (рис. 6.1, б), можно обнаружить, что верхние волокна при деформации изгиба балки удлиняются, а нижние укорачиваются. Очевидно, что можно найти такие волокна, длина которых остается неизменной. Совокупность волокон, не меняющих своей длины при изгибе балки, называется нейтральным слоем (н. с.). Нейтральный слой пересекает поперечное сечение балки по прямой, которая называетсянейтральной линией (н. л.) сечения. Для вывода формулы, определяющей величину нормальных напряжений, возникающих в поперечном сечении, рассмотрим участок балки в деформированном и не деформированном состоянии (рис. 6.2). Рис. 6.2 Двумя бесконечно малыми поперечными сечениями выделим элемент длиной . До деформации сечения, ограничивающие элемент, были параллельны между собой (рис. 6.2, а), а после деформации они несколько наклонились, образуя угол. Длина волокон, лежащих в нейтральном слое, при изгибе не меняется. Обозначим радиус кривизны следа нейтрального слоя на плоскости чертежа буквой. Определим линейную деформацию произвольного волокна, отстоящего на расстоянииот нейтрального слоя. Длина этого волокна после деформации (длина дуги ) равна. Учитывая, что до деформации все волокна имели одинаковую длину, получим, что абсолютное удлинение рассматриваемого волокна Его относительная деформация Очевидно, что , так как длина волокна, лежащего в нейтральном слое не изменилась. Тогда после подстановкиполучим (6.2) Следовательно, относительная продольная деформация пропорциональна расстоянию волокна от нейтральной оси. Введем предположение, что при изгибе продольные волокна не надавливают друг на друга. При таком предположении каждое волокно деформируется изолировано, испытывая простое растяжение или сжатие, при котором . С учетом (6.2) , (6.3) т. е. нормальные напряжения прямо пропорциональны расстояниям рассматриваемых точек сечения от нейтральной оси. Подставим зависимость (6.3) в выражение изгибающего момента в поперечном сечении (6.1) . Вспомним, что интегралпредставляет собой момент инерции сечения относительно оси . Или (6.4) Зависимость (6.4) представляет собой закон Гука при изгибе, поскольку она связывает деформацию (кривизну нейтрального слоя ) с действующим в сечении моментом. Произведениеносит название жесткости сечения при изгибе, Н·м2. Подставим (6.4) в (6.3) (6.5) Это и есть искомая формула для определения нормальных напряжений при чистом изгибе балки в любой точке ее сечения. Для того, чтобы установить, где в поперечном сечении находится нейтральная линия подставим значение нормальных напряжений в выражение продольной силыи изгибающего момента Поскольку , ; то (6.6) (6.7) Равенство (6.6) указывает, что ось – нейтральная ось сечения – проходит через центр тяжести поперечного сечения. Равенство (6.7) показывает что и- главные центральные оси сечения. Согласно (6.5) наибольшей величины напряжения достигают в волокнах наиболее удаленных от нейтральной линии Отношение представляет собой осевой момент сопротивления сеченияотносительно его центральной оси, значит Значение для простейших поперечных сечений следующее: Для прямоугольного поперечного сечения , (6.8) где - сторона сечения перпендикулярная оси; - сторона сечения параллельная оси; Для круглого поперечного сечения , (6.9) где - диаметр круглого поперечного сечения. Условие прочности по нормальным напряжениям при изгибе можно записать в виде (6.10) Все полученные формулы получены для случая чистого изгиба прямого стержня. Действие же поперечной силы приводит к тому, что гипотезы, положенные в основу выводов, теряют свою силу. Однако практика расчетов показывает, что и при поперечном изгибе балок и рам, когда в сечении кроме изгибающего момента действует еще продольная силаи поперечная сила, можно пользоваться формулами, приведенными для чистого изгиба. Погрешность при этом получается незначительной. studfiles.net σ — нормальные напряжения,τ — касательные напряжения,Qy – внутренняя поперечная сила,Mx – внутренний изгибающий момент,Ix – осевой момент инерции сечения балки,Wx – осевой момент сопротивления сечения,[σ], [τ] – соответствующие допустимые напряжения,E – модуль упругости I рода (модуль Юнга),y — расстояние от оси x до рассматриваемой точки сечения балки. Расчет внутренних поперечных сил и изгибающих моментов Формула кривизны балки в заданном сечении Расчет нормальных напряжений в произвольной точке сечения балки Условие прочности по нормальным напряжениям при изгибе (проверочный расчет) Осевые моменты инерции I и сопротивления W Касательные напряжения в произвольной точке сечения определяются по формуле Журавского: Здесь: Sx* — статический момент относительно оси x отсеченной части сечения b — ширина сечения на уровне рассматриваемой точки Условие прочности балки по касательным напряжениям Дифференциальное уравнение линии изогнутой оси балки Уравнения метода начальных параметров (МНП) θz, yz — соответственно угол наклона и прогиб сечения балки на расстоянии z от начала координат,θ0, y0 — соответственно угол наклона и прогиб сечения балки в начале координат,m, F, q — соответственно все изгибающие моменты, сосредоточенные силы и распределенные нагрузки приложенные к балке,a, b — расстояние от начала координат до сечений где приложены моменты и силы соответственно,c — расстояние от начала координат до начала распределенной нагрузки q. Другие формулы >Примеры решения задач >Краткая теория > isopromat.ru Косым изгибом называется такой случай изгиба, при котором плоскость действия нагрузки не совпадает ни с одной из главных осей инерции сечения. Рассмотрим случай, когда к сечению бруса под некоторым углом приложена сила P. При решении таких задач силу Р раскладывают на составляющие Рх и Ру и затем пользуются принципом независимости действия сил: Изгибающие моменты в сечении 1-1: Нормальные напряжения в общем случае: Очевидно, что можно найти такую линию, на которой суммарные напряжения равны нулю. Такая линия называется нейтральной (или нулевой), текущие координаты x и y: Так как Из этих формул следует, что нейтральная линия в сечении, в общем случае, не перпендикулярна следу плоскости действия в том же сечении результирующего изгибающего момента. Эти линии будут перпендикулярны при условии равенства углов α и φ. А это возможно в следующих случаях: Для таких сечений, у которых центральные оси главные (квадрат ,круг и т.п.), косой изгиб невозможен. Нейтральная линия делит поперечное сечение на две области: растянутую и сжатую. Проводя линии, параллельные нейтральной и касательной к контуру поперечного сечения, находим в той и другой области наиболее удалённые от нейтральной линии точки О1 и О2 с наибольшими растягивающими и сжимающими напряжениями: Определим напряжение в одной из точек Определим прогибы при косом изгибе. Прогибы определяются отдельно от составляющих Рх и Ру, затем определяется общее перемещение: Определим направление суммарного перемещения: Если проанализировать формулы (6) и (3), то можно отметить ,что направление прогибов перпендикулярно к нулевой линии и вместе с тем направление прогибов не совпадает с направлением действующей силы. Если нагрузка представляет плоскую систему сил, то ось изогнутого бруса лежит в плоскости, которая не совпадает с плоскостью действующих сил. Поэтому изгиб и называется косым. В случае действия пространственной системы сил ось изогнутого стержня представляет пространственную кривую. www.prosopromat.ruЛекции и примеры решения задач механики. Сопромат изгиб
Изгиб | ПроСопромат.ру
 В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.
В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.
 Изгибающий момент представляет собой результирующий момент внутренних нормальных сил
Изгибающий момент представляет собой результирующий момент внутренних нормальных сил , возникающих на бесконечно малых площадках и может быть выражен в интегральном виде:
, возникающих на бесконечно малых площадках и может быть выражен в интегральном виде:  (1), где y — плечо элементарной силы относительно оси х
(1), где y — плечо элементарной силы относительно оси х
 . Длина отрезка волокон нейтрального слоя при этом не изменится и будет равна:
. Длина отрезка волокон нейтрального слоя при этом не изменится и будет равна: , где
, где  -это радиус кривизны изогнутой оси балки. А вот любое другое волокно, лежащее ниже или выше нейтрального слоя, изменит свою длину. Вычислим относительное удлинение волокон, находящихся от нейтрального слоя на расстоянии у. Относительное удлинение — это отношение абсолютной деформации к первоначальной длине ,тогда:
-это радиус кривизны изогнутой оси балки. А вот любое другое волокно, лежащее ниже или выше нейтрального слоя, изменит свою длину. Вычислим относительное удлинение волокон, находящихся от нейтрального слоя на расстоянии у. Относительное удлинение — это отношение абсолютной деформации к первоначальной длине ,тогда: Сократим на
Сократим на и приведем подобные члены, тогда получим:
и приведем подобные члены, тогда получим: (2) Эта формула выражает геометрическую сторону задачи о чистом изгибе: деформации волокон прямо пропорциональны их расстояниям до нейтрального слоя.
(2) Эта формула выражает геометрическую сторону задачи о чистом изгибе: деформации волокон прямо пропорциональны их расстояниям до нейтрального слоя.  , тогда с учетом формулы (2) имеем
, тогда с учетом формулы (2) имеем (3),т.е. нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Подставим (3) в уравнение (1) и вынесем за знак интеграла дробь
(3),т.е. нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Подставим (3) в уравнение (1) и вынесем за знак интеграла дробь  как постоянную величину, тогда имеем
как постоянную величину, тогда имеем . Но выражение
. Но выражение  - это осевой момент инерции сечения относительно оси х - Iх. Его размерность см4, м4
- это осевой момент инерции сечения относительно оси х - Iх. Его размерность см4, м4 ,откуда
,откуда (4) ,где
(4) ,где - это кривизна изогнутой оси балки, а
- это кривизна изогнутой оси балки, а - жесткость сечения балки при изгибе.
- жесткость сечения балки при изгибе. (5)
(5)  (6) называют осевым моментом сопротивления сечения. Его размерность см3, м3. Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений.
(6) называют осевым моментом сопротивления сечения. Его размерность см3, м3. Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений. (7)
(7) (8)
(8) Подставим сюда формулу нормальных напряжений (3) и получим
Подставим сюда формулу нормальных напряжений (3) и получим Так как модуль продольной упругости материала балки не равняется нулю и изогнутая ось балки имеет конечный радиус кривизны, остается положить, что
Так как модуль продольной упругости материала балки не равняется нулю и изогнутая ось балки имеет конечный радиус кривизны, остается положить, что  этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной линии-оси х
этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной линии-оси х  , и, поскольку он равен нулю, то нейтральная линия проходит через центр тяжести сечения.
, и, поскольку он равен нулю, то нейтральная линия проходит через центр тяжести сечения. (отсутствие момента внутренних сил относительно силовой линии) даст
(отсутствие момента внутренних сил относительно силовой линии) даст или с учетом (3)
или с учетом (3)  . По тем же соображениям (см. выше)
. По тем же соображениям (см. выше)  . В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр прямом изгибе взаимно перпендикулярны.
. В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр прямом изгибе взаимно перпендикулярны. 
Сопротивление материалов. Изгиб.
Сопротивление материалов
Изгиб
Основные понятия об изгибе
Чистый и поперечный изгиб балки
Изгибающий момент и поперечная сила
Понятие о деформации изгиба | ПроСопромат.ру






 , где н.о. — это нейтральная ось
, где н.о. — это нейтральная ось
 Нормальное напряжение равно отношению максимального изгибающего момента к осевому моменту сопротивления сечения относительно нейтральной оси.
Нормальное напряжение равно отношению максимального изгибающего момента к осевому моменту сопротивления сечения относительно нейтральной оси. , где
, где - это статический момент площади отсеченной части.
- это статический момент площади отсеченной части. , Максимальное касательное напряжение равно отношению: в числителе произведение максимального значения поперечной силы на статический момент площади отсеченной части; в знаменателе произведение осевого момента инерции относительно нейтральной оси на ширину рассматриваемого сечения.
, Максимальное касательное напряжение равно отношению: в числителе произведение максимального значения поперечной силы на статический момент площади отсеченной части; в знаменателе произведение осевого момента инерции относительно нейтральной оси на ширину рассматриваемого сечения.Задачи на изгиб | ПроСопромат.ру


 Определим необходимое расчетное значение осевого момента сопротивления сечения:
Определим необходимое расчетное значение осевого момента сопротивления сечения:

 Тогда получим недонапряжение:
Тогда получим недонапряжение:











 (в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)
(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)













Чистый изгиб. Поперечный изгиб. Общие понятия.
Нормальные напряжения и деформации при чистом изгибе.
Формулы для расчетов на изгиб




 h – высота сечения,b – ширина сечения балки.
h – высота сечения,b – ширина сечения балки. D — диаметр сечения
D — диаметр сечения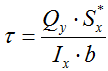



Косой (сложный) изгиб | ПроСопромат.ру



 (1)
(1) (2)
(2) (3)
(3) ,т.е.когда
,т.е.когда  - угол между силовой и нулевой линией прямой, а это значит, что любая центральная ось сечения является главной осью ,значит ,изгиб будет прямым.
- угол между силовой и нулевой линией прямой, а это значит, что любая центральная ось сечения является главной осью ,значит ,изгиб будет прямым.
 (4)
(4) (5)
(5) (6)
(6)











