Строительные работы в Севастополе
Некоторая установка, выделяющая мощность 30 кВт, охлаждается проточной водой, текущей по спиральной трубке диаметром 15 мм. При установившемся режиме проточная вода нагревается на 15 °C. Определить скорость воды, предполагая, что вся выделяемая мощность установки идет на нагрев воды. Задача №5.1.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ» \(N=30\) кВт, \(d=15\) мм, \(\Delta t=15^\circ\) C, \(\upsilon-?\) За некоторое малое время \(\tau\) установка выделяет количество теплоты \(Q\), которое можно найти по формуле: \[Q = N\tau \] Так как вся теплота идет на изменение температуры воды в трубке, то справедлива формула: \[Q = cm\Delta t\] Значит: \[N\tau = cm\Delta t\;\;\;\;(1)\] Здесь \(c\) — удельная теплоёмкость воды, равная 4200 Дж/(кг·°C), \(m\) — масса воды, которая протекла по трубке за время \(\Delta t\). Последнюю следует определять так: \[m = \rho V\;\;\;\;(2)\] В этой формуле \(\rho\) — плотность воды, равная 1000 кг/м3, \(V\) — объем протекшей воды. Последний равен объему трубки, который займёт вода за время \(\tau\), поэтому: \[V = Sl = \frac{{\pi {d^2}\upsilon \tau }}{4}\] Тут \(S\) — площадь сечения трубки (\(S = \frac{{\pi {d^2}}}{4}\)), \(l\) — расстояние, пройденное водой в трубке за время \(\tau\) (\(l = \upsilon \tau\)). Учитывая (2), имеем: \[m = \frac{1}{4}\rho \pi {d^2}\upsilon \tau \] Полученное выражение подставим в равенство (1): \[N\tau = \frac{1}{4}\rho \pi {d^2}\upsilon \tau c\Delta t\] \[N = \frac{1}{4}\rho \pi {d^2}\upsilon c\Delta t\] Откуда искомую скорость воды \(\upsilon\) следует искать по формуле: \[\upsilon = \frac{{4N}}{{c\rho \pi {d^2}\Delta t}}\] Переведём диаметр \(d\) в систему СИ: \[15\;мм = 0,015\;м\] Численный ответ задачи такой: \[\upsilon = \frac{{4 \cdot 30 \cdot {{10}^3}}}{{4200 \cdot 1000 \cdot 3,14 \cdot {{0,015}^2} \cdot 15}} = 2,7\;м/с = 9,7\;км/ч\] Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий. Если Вам понравилась задача и ее решение, то Вы можете поделиться ею с друзьями с помощью этих кнопок. easyfizika.ru Задача: Агрегат мощностью 50 кВт охлаждается проточной водой, текущей со скоростью 4 м/с по охватывающей агрегат трубке радиусом 5 см. Начальная температура воды 10 °С. До какой температуры нагревается вода, если половина тепловой мощности агрегата идет на ее нагревание? Удельная теплоемкость воды 4200 Дж/(кг · К). Пояснение: Обозначим N мощность агрегата, v — скорость течения, R — радиус трубы, t1 — начальную температуру воды, с — удельную теплоемкость воды, η — КПД агрегата, t2 — конечную температуру воды, Qпол — количество теплоты, пошедшее на нагревание воды, Qзатр — количество теплоты, выделяемое агрегатом, ρ — плотность воды, V — ее объем, l — длину столбика воды, t — время, за которое некоторое сечение этого столбика воды перемещается на длину l, m — массу протекающей по трубке воды. Здесь Qпол — количество теплоты, пошедшее на нагревание воды, Задача в общем виде решена. Выразим величины мощ- ности и радиуса в единицах СИ:5 кВт = 5 · 103 Вт,5 см = 5 · 10–2 м. Произведем вычисления: Ответ: t2 = 89,6 °С. otvetto.ru Скорость течения воды через трубку: где u - скорость воды, V - объем воды, S - сечение трубки, t -время. Объем воды можно выразить через ее массу и плотность: Массу воды, необходимой для отбора тепловой энергии от установки, определим исходя из количества теплоты вырабатываемой установкой: где Q - количество теплоты (оно в нашем случае равно мощности установки N, умноженной на время работы установки t), C - удельная теплоемкость воды, m - масса воды, dT - прирост температуры. Тогда из (3) следует (4): С учетом (4) и (2) формулу (1) можно переписать в виде: 1 Ватт*с = 1 Джоуль, плотность воды p=1000 кг/м^3. ivandriver.blogspot.comЗадачи по физике решаем вместе. Установка выделяющая тепловую мощность 50 квт охлаждается проточной водой
Некоторая установка, выделяющая мощность 30 кВт, охлаждается проточной водой
Условие задачи:
Дано:
Решение задачи:
Ответ: 9,7 км/ч.
Агрегат мощностью 50 кВт охлаждается проточной водой, текущей со скоростью 4 м/с по охватывающей агрегат трубке


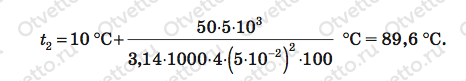
Задачи по физике решаем вместе
Некоторая установка, развивающая мощность 30 кВт, охлаждается проточной водой, текущей по спиральной трубке сечением 1 см2. При установившемся режиме проточная вода нагревается на 15 С. Определите скорость течения воды (в м/с), предполагая, что вся энергия, выделяющаяся при работе установки, идёт на нагревание воды. Удельная теплоёмкость воды 4200 Дж/(кг С).