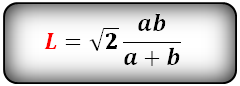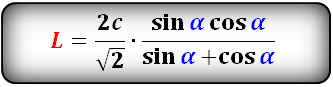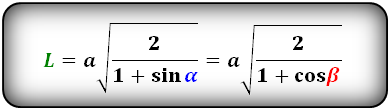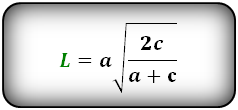Строительные работы в Севастополе
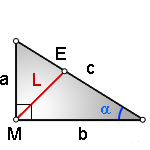
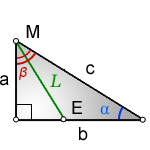
Зная стороны треугольника, можно найти все остальные его параметры по выведенным для треугольника формулам, просто подставив их значения. Периметр треугольник будет представлять собой сумму всех его сторон, а площадь выводится по формуле Герона, как квадратный корень из произведения полупериметра на его разность с каждой стороной по очереди, и деленному на два. P=a+b+c S=√(p(p-a)(p-b)(p-c)/2) Все углы в треугольнике, зная стороны, можно найти через теорему косинусов. (рис.75) cosα=(b^2+c^2-a^2)/2bc В произвольном треугольнике также есть три медианы m (делящие противоположную сторону пополам), три биссектрисы l (делящие угол пополам) и три высоты h (перпендикуляры из угла к стороне или ее проекции). Все их можно вычислить, имея в распоряжении значения трех сторон. Формула медианы, которая опущена на сторону c.(рис.75.1) m_c=√(2a^2+2b^2-c^2 )/2 Найти медиану, опущенную на сторону a или b, можно заменив необходимые стороны в формуле так, чтобы сторона, поделенная медианой пополам, была со знаком «–». m_a=√(2b^2+2c^2-a^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2 Формула биссектрисы, которая выходит из угла γ и опущена на сторону с. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b) Чтобы найти биссектрисы, которые выходят из двух других углов, нужно преобразовать формулу аналогично формуле медианы, где противоположная сторона со знаком «–». l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c) Формула высоты, которая опущена на сторону a, b или c видоизменяется таким образом, чтобы в знаменателе была нужная сторона.(рис.75.3) h_a=(2√(p(p-a)(p-b)(p-c) ))/a h_b=(2√(p(p-a)(p-b)(p-c) ))/b h_c=(2√(p(p-a)(p-b)(p-c) ))/c Также в любом треугольнике можно провести среднюю линию, которая также как медиана обозначается буквой m, поэтому для их разделения, будем использовать заглавную M для средней линии. Средняя линия параллельна той стороне, которая выбрана основанием треугольника, и равна ее половине. Среди свойств средней линии можно отметить, что боковые стороны она делит на две равные части, поэтому если начертить все три средние линии в треугольнике, то получится еще один треугольник, подобный первому, в два раза меньше. (рис. 75.7) M_a=a/2 M_b=b/2 M_c=c/2 В каждый треугольник можно вписать окружность и описать ее вокруг него. Центр вписанной в треугольник окружности будет находиться на пересечении его биссектрис, а радиус будет опущен под прямым углом к любой стороне и его формула выводится также по Герону. (рис.75.5) r=√(((p-a)(p-b)(p-c))/p) Центр описанной вокруг произвольного треугольника окружности находится на пересечении его медиатрисс (срединных перпендикуляров, радиус опущен в любую вершину или угол, и вычисляется по следующей формуле. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c))) geleot.ru Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла — sin(A), Косинус угла — cos(A), Тангенс угла — tg(A), Котангенс угла — ctg(A), Секанс угла — sec(A), Косеканс угла — cosec(A). Решение прямоугольного треугольника Второй катет b определится по теореме Пифагора: \[ b = \sqrt{c^2 - a^2} \] Угол A определится по формуле синуса: \[ \sin(A) = \frac{a}{c} \] Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так: \[ B = 180° - 90° - A \] Гипотенуза с определится по теореме Пифагора: \[ c = \sqrt{a^2 + b^2} \] Угол A определится по формуле тангенса: \[ \tg(A) = \frac{a}{b} \] Поскольку сумма всех углов треугольника равна 180° то второй острый угол определится так: \[ B = 180° - 90° - A \] Если дан острый угол A, то B найдется по формуле: \[ B = 90° - A \] Стороны можно найти по следующим формулам: \[ a = c · \sin(A) \] \[ b = c · \cos(A) \] \[ a = b · \tg(A) \] \[ b = c · \sin(B) \] \[ a = c · \cos(B) \] \[ b = a · \tg(B) \] \[ c = \frac{a}{\sin(A)} \] \[ c = \frac{b}{\cos(A)} \] \[ b = \frac{a}{\tg(A)} \] Здесь все углы мы найдем по формуле (7). Гипотенузу по формуле (14) и второй катет по формуле (16). www.fxyz.ru В прямоугольном треугольнике, зная катеты, можно найти гипотенузу через теорему Пифагора. Для этого нужно извлечь квадратный корень из суммы квадратов катетов. с=√(a^2+b^2 ) Площадь прямоугольного треугольника равна половине произведения катетов, а периметр – сумме катетов и гипотенузы. S=ab/2 P=a+b+c=a+b+√(a^2+b^2 ) Углы в прямоугольном треугольнике найти, зная катеты, тоже невероятно просто. Отношение одного катета к другому будет тангенсом противоположного угла и котангенсом близлежащего. (рис. 79.1) tanα=a/b cotα=a/b С другой стороны, зная один из углов, можно найти второй, отняв его из 90 градусов. α=90°-β Высота у прямоугольного треугольника всего одна, и она относится к любому из катетов как косинус прилежащего к нему угла. (рис. 79.2) cosα=h/b h=b cosα cosβ=h/a h=a cosβ Формула медианы в прямоугольном треугольнике преобразуется в отношение гипотенузы к двум или радикала из суммы квадратов катетов к двум, если даны только катеты. (рис. 79.3) m_c=√(2a^2+2b^2-c^2 )/2=√(2c^2-c^2 )/2=√(c^2 )/2=c/2=√(a^2+b^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2 m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4b^2+a^2 )/2 Биссектриса, опущенная на гипотенузу, вычисляется аналогично произвольному треугольнику, с подстановкой радикала вместо гипотенузы. (рис.79.4) l_c=√(ab(a+b+c)(a+b-c))/(a+b)=√(ab((a+b)^2-с^2))/(a+b)=√(ab(a^2+2ab+b^2-a^2-b^2))/(a+b)=√(ab*2ab)/(a+b)=(ab√2)/(a+b) l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b-c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c) Средние линии прямоугольного треугольника образуют внутри него еще один прямоугольный треугольник. Внутренний треугольник будет подобен внешнему, так как средние линии параллельны катетам и гипотенузе, и равны соответственно их половинам. Поскольку гипотенуза неизвестна, для нахождения средней линии M_c нужно подставить радикал из теоремы Пифагора. (рис.79.7) M_a=a/2 M_b=b/2 M_c=c/2=√(a^2+b^2 )/2 Радиус вписанной окружности в прямоугольном треугольнике вычисляется по упрощенной формуле для произвольного треугольника, а радиус описанной окружности является половиной гипотенузы и совпадает с медианой. (рис. 79.5, 79.6) r=(a+b-c)/2=(a+b-√(a^2+b^2 ))/2 R=m=c/2=√(a^2+b^2 )/2 geleot.ru Венцом строительства дома всегда является кровля, и какой она будет, зависит не только от пожелания домовладельца, но и от того, как рассчитать угол наклона крыши. Установка стропильных ног обычно не вызывает трудностей, если есть необходимые крепежные элементы, однако, выверяя угол, под которым будут уложены скаты, можно ошибиться, если не знать некоторых тонкостей. Например, очень высокая кровля в местности с сильными ветрами будет постоянно подвергаться большим нагрузкам и в итоге с большой долей вероятности будет разрушена. Следовательно, чтобы этого избежать, иногда стоит отдать предпочтение не слишком эффектной, но устойчивой низкой крыше. Таких примеров можно привести множество, но рассмотрим сами факторы, влияющие на высоту кровли. От чего она может зависеть? Как уже стало ясно, перед тем, как рассчитать угол наклона крыши, в первую очередь необходимо принять во внимание климатические особенности региона. Так, например, чем острее двускатная крыша, тем хуже на ней удерживается снег и легче стекает с нее дождевая вода. Однако, чем чреват такой крутой уклон, при сильном ветре, мы уже знаем. В тех местах, где жаркое солнце, лучше возводить скаты с минимальным уклоном или вообще обойтись без них, то есть сделать плоской поверхность кровли, которая тем сильнее получает и передает вниз тепло, чем больше ее площадь. Последняя увеличивается пропорционально крутизне уклона. Чем более полога крыша, тем выше вероятность того, что сильными порывами ветра с дождем влага будет загоняться под края кровельного покрытия. Помимо прочего, следует учитывать, каким образом будет использоваться пространство под стропильной системой – как чердак или в качестве жилой мансарды. В первом случае допускается расстояние до конька меньше среднего роста человека. Во втором случае необходимо, чтобы было достаточно комфортного пространства для передвижения, то есть просвет в центре помещения должен составлять не менее 2.5 метров и, желательно, не менее полутора метров в самой нижней точке потолка. Немалое воздействие на угол ската крыши может оказать материал покрытия, который можно укладывать только при определенной степени крутизны наклона. Самое важное в любом помещении – его полезная площадь, то есть та, которую можно будет использовать для расстановки мебели и передвижения, а также для хранения вещей. В мансарде иногда бывает сложно использовать некоторые участки пространства, где располагается самая низкая точка потолочной обшивки. Впрочем, такие места как раз можно отвести под хранение вещей, сделав там встроенные шкафчики и тумбы. Другое дело – зона свободного передвижения, ее площадь напрямую зависит от высоты конька, а значит – и угла крыши. Рассмотрим на примере. Допустим, ширина дома – 9.5 метров. Если хочется простора над головой в пределах 3 метров хотя бы по центру комнаты, то угол между скатами должен быть не менее 35 градусов, поскольку уже при 30 высота конька окажется чуть больше 2.5 метров. Однако следует учитывать, что тогда ширина пространства, доступного для свободного передвижения (до двухметрового уровня потолка), окажется немногим больше 3.5 метров. Если придерживаться той же высоты в самых низких точках наклонного потолка, и при этом сделать угол кровли 30 градусов, то ширина комнаты сократится до 2.4 метров. Наиболее комфортно будет в мансарде под крышей с углом более 40 градусов, однако следует учитывать, что у такой конструкции, в сравнении с пологим скатом (около 10 градусов), ветровая нагрузка увеличивается почти в 5 раз. В целом, зависимость угла наклона кровли от высоты конька только облегчает расчеты стропильной системы. Однако для вычислений нужно достаточно хорошо знать азы геометрии. Чаще всего, сечение конструкции крыши со стороны фронтонов представляет собой треугольник, равносторонний, равнобедренный или иного типа. Соответственно, пользуясь простейшими формулами, можно вычислить длину любой стороны и сопредельный с ней угол, зная основание и высоту. При этом нам, помимо измерительной рулетки, понадобится таблица Брадиса, поскольку придется столкнуться с тангенсами. Итак, смотрим на фронтон и видим равносторонний треугольник, состоящий из двух прямоугольных, один из катетов для которых является общим. Существует формула, согласно которой тангенс угла А при основании равен отношению противолежащего катета к прилежащему, то есть, Tg A = H/(L/2). Иными словами, в нашем случае это высота H, деленная на половину основания L. Возьмем ту же ширину фронтона 9.5 метров, половина его будет соответствовать 4.75, на это значение делим высоту конька, которую сочтем комфортной, например, 4 метра. В итоге получаем 4/4.75 = 0.84, заглядываем в таблицу Брадиса, ищем соответствующую позицию в таблице тангенсов и видим, что нам нужен угол 40°. Любая кровля – это своего рода слоеный пирог из гидро- и пароизоляции, утеплителя, обрешетки и внешнего покрытия. Все это уложено на стропильную систему под определенным углом, который ограничивает использование того или иного материала. Главным образом следует ориентироваться на инструкции, предложенные изготовителем, которые касаются и требований к уклону скатов. Кровельные материалы бывают рулонные, наборные (черепица и шифер), листовые, а также гибкие штучные, и для каждого типа предусмотрен минимальный угол крыши. Для рулонных покрытий оптимальным считается уклон не более 15 градусов при условии, что материал укладывается в 2 слоя. Если же кровля делается трехслойной, она должна быть еще более пологой, около 5 градусов, при этом требуется дополнительная обрешетка для повышения прочности на случай увеличения временной нагрузки (снег, дождь). Но есть и исключение – мембранное покрытие, которое можно использовать при любом наклоне крыши. Наборные материалы также не терпят крутых скатов, по той простой причине, что могут съехать под собственной тяжестью при малейшей предпосылке к этому, вроде штормового порыва ветра. Однако и слишком маленьким угол делать нельзя, поскольку в этом случае масса кровельного материала будет излишне нагружать опорные конструкции, то есть стропила, обрешетку и прочие элементы. Оптимальным считается угол 22 градуса, достаточной для того, чтобы во время дождя влага свободно стекала и не задувалась ветром под стыки. В отношении профнастила и металлочерепицы минимальный уклон – 12 и 14 градусов соответственно, достаточно пологий, чтобы осадки стекали с крыши, и при этом не нарушалась ее герметичность на стыках. В большую сторону крутизна может увеличиваться без ограничений, однако с учетом того, что большая площадь кровли имеет солидную массу. Также не следует забывать про ветровую нагрузку и высокую парусность крыш с углом, близким к 45 градусам. Оптимальный наклон – порядка 27-30 градусов. А вот у мягкой черепицы, которая состоит из отдельных кусков материала типового размера, угол кровли связан с плотностью обрешетки. Если скаты очень пологие, то расстояние между планками следует сделать как можно меньше. Это обусловлено тем, что снеговые массы могут стать непосильной нагрузкой для покрытия. В том случае, когда крутизна скатов выдержана в пределах 30-40 градусов, шаг обрешетки допускается больший, до 45 сантиметров. remoskop.ru Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2 Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4 Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cosα=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cosβ=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 ) Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2 В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b) Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2 Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b)) Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 ) geleot.ru Крыша дома должна быть надежной и красивой, а возможно это при правильном определении ее угла наклона для данного вида кровельного материала. Как рассчитать угол наклона крыши — в статье. Содержание статьи Перед расчетом угла наклона крыши надо определиться с тем, как будет использоваться чердачное помещение. Если вы планируете сделать его жилым, угол наклона придется делать большим — чтобы помещение было просторнее, а потолки выше. Второй выход — делать ломанную, мансардную кровлю. Чаще всего такую крышу делают из двухскатной, но может она иметь и четыре ската. Просто во втором варианте очень уж сложной получается стропильная система и без опытного проектировщика просто не обойтись, а большинство предпочитает делать все самостоятельно, своими руками. Чем выше конек, тем больше полезная площадь подкровельного пространства. Но одновременно увеличивается и площадь крыши При увеличении угла уклона кровли стоит помнить несколько вещей: Угол наклона отображен через отношение высоты конька и половины ширины здания Это не значит, что крыши с малым уклоном лучше. Они обходятся по материалам дешевле — меньше площадь кровли, но имеют свои нюансы: Так что кровли с малым уклоном — тоже не подарок. Вывод: рассчитать угол наклона крыши надо так, чтобы найти компромисс между эстетической составляющей (дом должен смотреться гармонично), практической (при жилом подкровлельном пространстве) и материальной (расходы необходимо оптимизировать). Крыша на доме может иметь практически любой вид — может иметь низкие скаты, может — почти отвесные. Важно при этом правильно рассчитать ее параметры — сечение стропильных ног и шаг их установки. Если вы хотите уложить на крышу определенный вид кровельного материала, принимать во внимание надо такой показатель, как максимальный и минимальный угол наклона для данного материала. Минимальные углы прописаны в ГОСТе (смотрите таблицу выше), но часто производители дают свои рекомендации, так что желательно определиться с конкретной маркой еще на стадии проектирования. Чаще угол ската крыши часто определяют исходя из того, как сделаны они у соседей. С практической точки зрения это правильно — условия у близлежащих домов аналогичны, и, если соседские крыши стоят хорошо, не текут, можно взять за основу их параметры. Если же по соседству нет крыш с тем кровельным материалом, который вы планируете использовать, можно начать расчеты со средних значений. Они приведены в следующей таблице. Как видите, в графе «как делают» в большинстве случаев есть солидный диапазон. Так что имеется возможность варьировать внешний вид здания даже с одинаковой крышей. Ведь кроме практической роли крыша еще и украшение. И при выборе угла ее наклона немаловажную роль играет эстетическая составляющая. Сделать это проще в программах, дающих возможность отобразить объект в объемном изображении. Если воспользоваться этой методикой, то рассчитать угол наклона крыши в данном случае — выбрать его из определенного диапазона. На угол наклона кровли влияет количество снега, выпадающее за зиму в конкретном регионе. Также при проектировании учитываются ветровые нагрузки. Карта снеговых нагрузок РФ Все более-менее просто. По данным многолетних наблюдений вся территория РФ разделена на зоны с одинаковой снеговой и ветровой нагрузкой. Эти зоны нанесены на карты, закрашены разными цветами, так что ориентироваться несложно. По карте определяете местоположение дома, находите зону, по ней — значение ветровой и снеговой нагрузки. На карте снеговых нагрузок стоит две цифры. Первая используется при расчете прочности конструкции (наш случай), вторая — при определении допустимого прогиба балок. Еще раз: при расчете угла наклона кровли пользуемся первой цифрой. Основная задача расчета снеговых нагрузок — учесть планируемый уклон кровли. Чем круче скат, тем меньшее количество снега может на нем удержаться, соответственно, меньшее сечение стропил или больший шаг их установки потребуется. Для учета этого параметра вводятся поправочные коэффициенты: Как видим из списка коэффициентов, изменяется значение только на крышах с углом наклона 25° — 60°. Для остальных это действие смысла не имеет. Итак, чтобы определить действительную снеговую нагрузку на планируемую крышу, берем значение, найденное по карте, умножаем на коэффициент. И все это крыша должна выдержать Например, рассчитываем снеговую нагрузку для дома в Нижнем Новгороде, угол уклона кровли — 45°. По карте это 4-ая зона, со средней снеговой нагрузкой 240 кг/м2. Крыша с таким скатом требует корректировки — найденное значение умножаем на 0,7. Получаем 240 кг/м2 * 0,7 = 167 кг/м2. Это — только часть расчета угла наклона крыши. Влияние снега высчитать просто — чем больше снега в регионе, тем больше возможные нагрузки. Предсказать поведение ветра намного сложнее. Можно только ориентироваться на преобладающие ветра, местоположение дома и его высоту. Эти данные при расчете угла наклона кровли учитываются при помощи коэффициентов. Карта ветровых нагрузок РФ Положение дома относительно роза ветров имеет большое значение. Если дом стоит между более высокими зданиями, ветровые нагрузки будут меньше, чем в том случае, когда он находится на открытой местности. Все дома по типу расположения делят на три группы: Дом считается принадлежащим к данной зоне, если указанное окружение находится на расстоянии не менее 30-кратной высоты дома. Например, высота дома 3,3 метра. Если на расстоянии 99 метров (3,3 м * 30 = 99 м) находятся только небольшие одноэтажные дома или деревья, он считается принадлежащим к зоне «Б» (даже если территориально находится в крупном городе). В зависимости от зоны, вводятся коэффициенты, учитывающие высоту здания (приведены в таблице). Потом их используют при расчете ветровой нагрузки на крышу дома. Например, рассчитаем ветровую нагрузку для Нижнего Новгорода, одноэтажный дом находится в частном секторе — относится к группе «Б». По карте находим зону ветровых нагрузок — 1, ветровая нагрузка для нее 32 кг/м2. В таблице находим коэффициент (для зданий ниже 5 метров), он равен 0,5. Перемножаем: 32 кг/м2 * 0,5 = 16 кг/м2. Но это еще не все. Надо еще учесть аэродинамические составляющие ветра (при определенных условиях он стремиться сорвать крышу). В зависимости от направления ветра и его воздействия кровлю, ее делят на зоны. В каждой из них возникают разные нагрузки. В принципе, в каждой зоне можно ставить стропила разного размера, но так не делают — это неоправданно. Для упрощения расчетов рекомендуют брать показатели из самых нагруженных зон G и H (смотрите таблицы). Коэффициенты для учета аэродинамической составляющей ветровой нагрузки Найденные коэффициенты применяют к рассчитанной выше ветровой нагрузке. Если коэффициента два — с отрицательной и положительной составляющей, считается оба значения, а потом они суммируются. Найденные значения ветровых и снеговых нагрузок являются основой для расчета сечения стропильных ног и шага их установки, но не только. Суммарная нагрузка (вес конструкции кровли + снеговая + ветровая) не должна превышать 300 кг/м2. Если после всех расчетов сумма у вас получилась больше, надо или выбирать более легкие кровельные материалы, или уменьшать угол наклона кровли. Итак, выводы. Рассчитать угол наклона крыши — это, Скорее, выбрать один из возможных вариантов. Важно только чтобы выбор этот оказался правильным. stroychik.ru 1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу: L - биссектриса, отрезок ME , исходящий из прямого угла (90 град) a, b - катеты прямоугольного треугольника с - гипотенуза α - угол прилежащий к гипотенузе Формула длины биссектрисы через катеты, ( L): Формула длины биссектрисы через гипотенузу и угол, ( L): 2. Найти по формулам длину биссектрисы из острого угла на катет: L - биссектриса, отрезок ME , исходящий из острого угла a, b - катеты прямоугольного треугольника с - гипотенуза α, β - углы прилежащие к гипотенузе Формулы длины биссектрисы через катет и угол, (L): Формула длины биссектрисы через катет и гипотенузу, (L): www-formula.ruСтороны равнобедренного треугольника. Расчет угла
Стороны треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Решение прямоугольного треугольника | Формулы и расчеты онлайн
Решение прямоугольного треугольника по двум сторонам

Если известны катет a и гипотенуза c
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и гипотенуза)
Если известны катеты a и b
Вычислить, найти решение прямоугольного треугольника по двум сторонам (катет и катет)
Решение прямоугольного треугольника по стороне и острому углу
Вычислить, найти решение прямоугольного треугольника если известны катет a и противолежащий угол A
В помощь студенту
Решение прямоугольного треугольника
стр. 237
Катеты прямоугольного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Как рассчитать угол наклона крыши
Что нужно перед тем, как рассчитать угол наклона крыши?


Расчет необходимой величины пологости скатов мансарды

Калькулятор расчёта угла наклона крыши
Выберите 2 любых известных значения, введите их. Остальные значения будут рассчитаны автоматически.

Как материал может повлиять на наклон крыши?


Стороны равнобедренного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Как рассчитать угол наклона крыши с примерами
Назначение подкровельного пространства


Угол наклона в зависимости от кровельного материала
Наименование кровельного материалаМинимальный угол наклона (в градусах) Асбоцементный шифер и ондулин 6° Цементно-песчаная и керамическая черепица 10° Гибкая битумная черепица 12° Металлочерепица 6° Асбо-цементные или сланцевые плиты 27° Стальные оцинкованные, медные, цинк-титановые листы 17° Профнастил 6° Тип кровлеьного материалаРекомендуемый угол наклона минимальный/максимальныйКакой наклон ската делают чаще всего Кровля из толя с посыпкой 3°/30° 4°-10° Двухслойная толевая 4°/50° 6°-12° Цинковая с двойными стоячими фальцами 3°/90° 5°-30° Шпунтованная черепица с 4-мя желобками 18°/50° 22°-45° Голландская черепица 40°/60° 45° Обычная керамическая черепица 20°/33° 22° Профнастил и металлочерепица 18°/35° 25° Асбоцементный шифер 5°/90° 30° Искусственный шифер 20°/90° 25°-45° Солома или камыш 45°/80° 60°-70° Влияние климатических факторов

Расчет снеговых нагрузок

Расчет ветровых нагрузок

Высота зданияЗона "А"Зона "Б"Зона "В" менее 5 метров 0,75 0,5 0,4 от 5 м до 10 м 1,0 0,65 0,4 от 10 м до 20 м 1,25 0,85 0,55 
Все формулы для треугольника